Adaptive Euler - resolution of the Grand Challenge of aerodynamics: first principles, automated computation and error control in FEniCS, validation in HLPW, and prototype development toward aeroelasticity and FSI

• Today the industry does not trust aerodynamics simulation - calls it "Colorful Fluid Dynamics"
• Euler aerodynamics makes simulation reliable - direct simulation of natural laws
• You can now reliably design, optimize, certify and innovate aircraft, wind turbines, ships, etc. in the web browser, 100x faster and cheaper than industry standard.
• Strong NASA recognition of breakthrough Euler aerodynamics from NASA Branch Chief of Computational Aerodynamics Cetin Kiris (also leader of Volcano)
• Reproducible Open Source Digital Math/FEniCS setting is future-proof - editable, testable, extensible - see e.g. how Linux (with Red Hat as key commercial actor) has become fundamental technology that large part of industry is built on.
• Delivered as DigiMat online course, largest online course in Sweden with 30000+ participants.

Johan Jansson (jjan@kth.se), key collaboration with Kristoffer Wingstedt (prev. Saab AB now FOI)
http://icarusmath.com
http://digitalmath.org (research environment)

*Leonhard Euler [1707-1783] one of the greatest mathematicians in history.

References - NASA (Branch Chief Cetin Kiris, also leads Volcano) recognition of Euler

[W-030 = Johan Jansson's Icarus/KTH team]

"As good as it gets" statement from NASA

https://hiliftpw.larc.nasa.gov/Workshop4/presentations.html

Success Stories

1. Associate Prof. and Docent in Computational Math at KTH
2. Elected to IVA Royal Swedish Academy of Engineering Sciences 100-list
3. Highlighted by NASA/HiLiftPW and Fields Medalist
4. Commercial collaboration with SAAB - one of the leading aircraft companies in the world - leverage Adaptive Euler aerodynamics breakthrough
5. Structured collaboration with FOI Swedish Defense Research Agency
6. Leader of the advanced subgroup "WMLES and Beyond" in the NASA benchmarking workshop AePW-4/DPW-8
7. Pilot project with leading Formula 1 team, other leading aircraft companies
8. Johan Jansson and Icarus team co-founded FEniCS Open Source project - today de-facto world-standard for advanced math modeling - key component of Digital Math.
9. Highlighted by IVA and President of Association for Swedish Engineers as "possible solution to the crisis in Matte/STEM", and Teacher Magazine reaching all teachers in Sweden - close collaboration with Lidingö Municipality
10. DigiMat IVA Tekniksprånget - collaboration project reaching 1000s of high school graduates / year.
11. DigiMat Pro Sweden's largest online course 30000+ participants
12. H2020 MSO4SC (FEniCS HPC for industrial math), FP7 Eunison (FEniCS biomechanics), PRACE Tier-0 (highest level of EU HPC grant), organized panel debate with EC Open Science unit, etc.
13. ELISE project for electric aviation - predictive design with Heart Aerospace leading electric regional aircraft and drone startups in Sweden
14. Excellent feedback from course participants:
    Basic: "Super-fun way to learn math!", "I did not know so much about algoriths before, but now I've started to understand".
    Pro: "Cool!", "Very exciting!", "It is good that the Digital Math computational environment and the theory are combined together.", “Hands-on experience of manipulating codes that are applied in the real world engineering problem.”, 90% recommends course to others.

NASA Vision 2030

Slotnick, J. P., Khodadoust, A., Alonso, J., Darmofal, D., Gropp, W., Lurie, E., & Mavriplis, D. J. (2014). CFD vision 2030 study: a path to revolutionary computational aerosciences (No. NF1676L-18332).

The use of CFD in the aerospace design process is severely limited by the inability to accurately and reliably predict turbulent flows with significant regions of separation.

See also Certification by Analysis 2040 - we already now, 10-20 years ahead of time cover key aspects.

Methodology

• Proposed Adaptive Euler as solution to the NASA Vision 2030 challenges.
• Predictive incompressible Euler - first principles - no modeling parameters - free slip BC.
• Direct FEM cG(1)cG(1) in FEniCS with adjoint-based adaptive error control.
• Extremely fast and cheap: < 100 core hours - "zero" computational cost. 300x cheaper than industry standard "fastest" simulation technology RANS, 1000x-10000x cheaper than WMLES ("scale-resolving" technology)
• Coarse starting meshes for adaptive methodology from ANSA: 100k vertices giving good validation.
• Vision: Design and certification of aircraft and engineering systems should be done by simulation (e.g. Digital Math Real Flight Simulator) within 5 years.

HiLiftPW4 Prediction of CL and CD pre-stall within 5%, and CM for all angles and CL and CD at stall within 10%, spefically also predicts pitch-break.

Mesh-independent under adjoint-based adaptive error control

HiLiftPW4 CP plot for 21.5deg

Consistent with 5% accuracy vs. exp in forces, which are simply integrated CP.

Note oscillatory CP in in-board separation wake at A - captures the key separation mechanism.

Cylinder Re=Infinite starting from u=0

Resolution of D'Alembert's paradox: with unsteady Euler potential solution first establishes, but is unstable and develops into streamwise vortex solution, with non-zero drag close to experiment (see slides before)

Cylinder Re sweep from Re=4e3 to Re=Infinite (e.g. 1e7+)

Cylinder Re sweep from Re=4e3 to Re=Infinite (e.g. 1e7+)

Towards Adaptive Euler aeroelasticity - movie of elastic smoother mesh motion Adaptive Euler ALE

    def epsilon(v):
      return 0.5*(grad(v) + grad(v).T)

    rsmoother = inner(1.0/h*epsilon(wmeshvel), epsilon(vv))*dx + \
      gamma*nm*dot(wmeshvel - wmeshvelf, vv)*ds + gamma*im*dot(wmeshvel, vv)*dx
    newtonIteration(rsmoother, wmeshvel)
  

Try and edit yourself! Adaptive Euler Simple Wing ALE with elastic mesh smoothing: https://colab.research.google.com/drive/1WD8JOQxnvcCixCrf2YXAm13pariYf1ti?usp=sharing

Section: FEniCS

Automated Digital Math- realized in FEniCS

• Automated discretization: (generate code for linear system from PDE/model.)
  r = (inner(grad(u), grad(v)) - inner(f, v))*dx $\Rightarrow $ Poisson.cpp
  
  
• Automated error control: (including parallel adaptive mesh refinement.)
  Direct duality-based error control: $ M(\hat{e}) = r(\hat{U}, \hat{\phi})$
  
  $|M(e)| \le TOL \Rightarrow$
  
  with $M(e)$ a goal functional of the computational error $e = u - U$, and $\hat{\phi}$ the adjoint.
• Automated modeling of unresolved subscales: (i.e. turbulence)
  $(R(U), v) + h(R(U), R(v)) = 0, \forall v \in V_h$ (residual-based stabilization/dissipation)

Goal: Automatically generate the program, mesh and solution from PDE/model (residual) and goal functional $M(U)$ (e.g. drag).

First principles - Euler equations for fluid - slip boundary condition

Automated symbolic differentiation in FEniCS - Automated linearization as part of GLS stabilization

        # Automated linearization using derivative
        r_SD0 = derivative(d*inner(grad(u1)*u1, grad(u2)*u2)*dx, u1, u)
        r_SD1 = derivative(r_SD0, u2, v)
        r_SD1 = replace(r_SD1, { u1: u, u2: u })

        # Manual linearization
        r_SDA = r_SD1
        r_SDM = d*inner(grad(u)*u, grad(v)*u)*dx
  

Same values to machine precision.

Section: Adaptive Euler

HiLiftPW4 Prediction of CL and CD pre-stall within 5%, and CM for all angles and CL and CD at stall within 10%, spefically also predicts pitch-break.

Mesh-independent under adjoint-based adaptive error control

HiLiftPW4 CP plot for 21.5deg

Consistent with 5% accuracy vs. exp in forces, which are simply integrated CP.

Note oscillatory CP in in-board separation wake at A - captures the key separation mechanism.

Run and modify the simulations yourself in your web browser!

Solving the reproducibility crisis with Digital Math - "The Modern Scientific Paper". More detailed presentation and results:
http://digitalmath.tech/hiliftpw4-aiaa
Adaptive Euler Simple Wing: https://colab.research.google.com/drive/1rTTABf21r8Dd0pJLxNvFfsPSBl6q2H9t?usp=sharing
Adaptive Euler Simple Wing ALE with elastic mesh smoothing: https://colab.research.google.com/drive/1WD8JOQxnvcCixCrf2YXAm13pariYf1ti?usp=sharing

Adaptive Euler HLPW5 Case 2.2, 2.3, 2.4 preliminary forces

Our Adaptive Euler team achieved the target of prediction of key CLmax quantity within 2% of experiment in a blind setting (we did not have access to experimental data. Only 3 teams in WMLES group achiieved this: Adaptive Euler, Volcano (previous NASA branch chief) and PowerFlow. We also captured the key separation and stall phenomenon. Our performance is 300x cheaper than RANS and 1000x cheaper than WMLES.

Adaptive Euler HLPW5 Case 2.4 preliminary adaptive forces aoa=19.7

Variance CL and CD: ~3% 180k-230k vertices (appx. 5% increase of num. vertices each adaptive iter.)

Activity: Verification and uncertainty estimation.

Hypothesis: Mesh-cónverged forces already on coarsest starting mesh for all angles (iter_00).

Validation against oil flow for separation mechanism at stall angle (HLPW3)

The separation mechanism and validation looks similar for HLPW4 and 5

Our Adaptive Euler team achieved the target of prediction of key CLmax quantity within 2% of experiment in a blind setting (we did not have access to experimental data. Only 3 teams in WMLES group achiieved this: Adaptive Euler, Volcano (previous NASA branch chief) and PowerFlow. We also captured the key separation and stall phenomenon. Our performance is 300x cheaper than RANS and 1000x cheaper than WMLES.

Adaptive Euler HLPW5 forces blind validation and comparison to other participants

We observe a significant interaction of the wake with the tail at aoa=23.6 . We also observe a significant difference of appx. 15% in CM between "full span" and "half span", which we interpret as a "blockage effect".

This appears to be in principle a "buffeting" phenomenon.

Cylinder Re=Infinite starting from u=0

Resolution of D'Alembert's paradox: with unsteady Euler potential solution first establishes, but is unstable and develops into streamwise vortex solution, with non-zero drag close to experiment (see slides before)

Cylinder Re sweep from Re=4e3 to Re=Infinite (e.g. 1e7+)

Cylinder Re sweep from Re=4e3 to Re=Infinite (e.g. 1e7+)

Section: Aeroelasticity

Movie of elastic smoother mesh motion Adaptive Euler ALE

    def epsilon(v):
      return 0.5*(grad(v) + grad(v).T)

    rsmoother = inner(1.0/h*epsilon(wmeshvel), epsilon(vv))*dx + \
      gamma*nm*dot(wmeshvel - wmeshvelf, vv)*ds + gamma*im*dot(wmeshvel, vv)*dx
    newtonIteration(rsmoother, wmeshvel)
  

Try and edit yourself! Adaptive Euler Simple Wing ALE with elastic mesh smoothing: https://colab.research.google.com/drive/1WD8JOQxnvcCixCrf2YXAm13pariYf1ti?usp=sharing

Adaptive Euler DPW/AePW highlights and plan 1/3

• We emphasize our results are still a "development snapshot", we are developing and testing a new formulation.
• Ongoing uncertainty quantification.
• Case 1: We capture the main "transsonic buffet" phenomenon (large-magnitude shock oscillation) with Euler - free slip, zero friction, no boundary layer.
  Similar oscillation magnitude of appx. 5-10% of chord as in the main Jaquin et. al. reference.
  See e.g. the main Jaquin et. al. reference: "In transonic flow conditions, shock wave/turbulent boundary-layer interaction with separation may induce large- scale instabilities involving the whole flowfield and is known as transonic buffet"
  Our working hypothesis based on our very prelimniary results is that "transonic buffet" is not connected to the boundary layer, since we have no boundary layer.
• We appear to keep the very high efficiency we demonstrated in HLPW5, extremely coarse meshes and very large time steps, the total computational cost is appx. 1000 core hours for one simulation.
• Case 2 status: Very preliminary promising results with same high efficienc as shown in HLPW5 and for AePW/DPW Case 1. Extremely coarse mesh with appx. 100k vertices. We appear to capture the key stationary qualitative (very preliminary) and (very preliminary) quantitative phenomena, we have not yet started investigating the buffet phenomena. The total computational cost is appx. 1000 core hours for one simulation.
• In HLPW5 we demonstrated that we capture "wing wake-tail buffet", which is also of key importance for e.g. delta wings such as the FA-18 Hornet.

Adaptive Euler DPW/AePW highlights and plan 2/3

• Case 3 plan: Use our previously developed Unified Continuum FSI (UC-FSI) methodology/formulation with Adaptive Euler in the fluid phase. UC-FSI is simply a generalization of Adaptive Euler where we introduce a phase marker which selects constitutive law, and convection of the phase marker. Otherwise the methodology/formulation is the same: GLS-stabilized P1 space-time FEM in FEniCS with adjoint-based adaptive error control. UC-FSI means we discretize and solve for the entire momentum, density and energy fields for the entire FSI domain as one system - stabilization and adaptive error control automated and same for the entire system. Challenge to represent the discontinuity in the FSI interface in Adaptive Euler. We have a large body of previous work for UC-FSI for biomechanics where the FSI interface is continuous.

Adaptive Euler DPW/AePW highlights and plan 3/3

• Johan Jansson will present an overview of our Adaptive Euler activity in HLPW/DPW/AePW and industry activity at the FT2025 conference:
  https://ft2025.se/
  https://beyond-production.objects.dc-sto1.glesys.net/projects/9050e852-2137-4dd2-af9d-83d0262fb81f/documents/No8hATgof3fLaW8FdhrRVVnngfSgChDiogon3BJc.html

Similar shock structure and CP (very preliminary).
We use starting meshes from Helden, both for the Case 2 geometry and also from Case 2.1 from HLPW5 (CRM also with slat tracks and vertical stabilizer, which we modify ourselves, very similar to Case 2 geometry).

Direct FEM simulation of the compressible Euler equations with GLS stabilization in FEniCS - first principles - free slip - no modeling parameters..
Observations:
We appear to capture the key stationary qualitative (very preliminary) and (very preliminary) quantitative phenomena, we have not yet started investigating the buffet phenomena.

Similar shock structure and CP (very prelim).

Direct FEM simulation of the compressible Euler equations with GLS stabilization in FEniCS - first principles - free slip - no modeling parameters..
Observations:
We appear to capture the key stationary qualitative (very preliminary) and (very preliminary) quantitative phenomena, we have not yet started investigating the buffet phenomena.

The characteristic "delta wing leading edge vortices" for Soar2 (SAAB open model case) hitting the twin vertical tails. We make a preliminary observation of an interaction of the vortex wake with the tail, giving an oscillating pressure field (buffet). A plan forward is:
1. To carry out adaptive error control and uncertainty quantification.
2. To put the pressure loads on the tail in a structural context to see if there may be structural impact.
3. To put the pressure loads in a stability context to see if there may be impact of stability (e.g. pitching, rolling and yawing moments).
4. To explore a range of angles of attack and Mach numbers.

Similar oscillation magnitude of appx. 5-10% of chord as in the main Jaquin et. al. reference.

Direct FEM simulation of the compressible Euler equations with GLS stabilization in FEniCS - first principles - free slip - no modeling parameters..
Observations:
We appear to capture the key qualitative and (very preliminary) quantitative phenomena.

AePW/DPW submissions for Test Case 1b (Buffet). We (Adaptive Euler) appear to be the only submission from the EU.

Daumas, L., Chalot, F., Forestier, N., & Johan, Z. (2009). Industrial use of linearized CFD tools for aeroelastic problems. IFASD, 54, 21-25.

“The Galerkin/least-squares (GLS) formulation introduced by Hughes and Johnson, is a full space-time finite element technique …”

Unified Continuum (UC) modeling

Our UC methodology is a Direct FEM simulation of the first principle equations for Fluid-Structure Interaction (FSI), here in multi-phase incompressible form, where we include constitutive laws for a Newtonian fluid and Neo-Hookean solid that are active or not depending on the phase function/marker.

These first principle equations are discretized by the Direct FEM approach, meaning Galerkin-Least-Squares (GLS) stabilization with shock-capturing. A moving mesh (ALE) is part of the methodology, but is not necessary, below the mesh is fixed and the phase function convects across cells.

The Galerkin part of the UC method is formulated as below in FEniCS notation (where theta is a normalized rho, i.e. 0 for fluid and 1 for structure):

F_G = (inner(u, grad(rho))*nu)*dx
F_G += (inner(rho*grad(u)*u + grad(p),v) - theta*inner(sigma, grad(v)) + \
    (1 - theta)*nu*inner(grad(u),grad(v)) - rho*dot(f,v))*dx
F_G += (inner(dot(u, grad(sigma)) + \
    theta*(2*rho*mu*epsilon(u) + grad(u)*sigma + sigma*grad(u).T), y))*dx + \
F_G += (inner(div(u), q))*dx
  

Unified Continuum Fluid-Structure Interaction of flapping in FEniCS, simplified setting for conceptual purpose

Real Unified Continuum modeling

Vocal folds dynamic validation

Unified continuum simulation with realistic geometry of the human voice apparatus in the EUNISON project with turbulent fluid-structure interaction with aeroacoustics and parallel contact based on solving an Eikonal equation, generating self-oscillation of the vocal folds and the expected glottal wave pattern. Adaptive method validated for 3D FSI benchmark.

Real Unified Continuum modeling

Vocal folds dynamic validation

Unified Continuum Fluid-Structure Interaction - fixed-mesh variant, implicit/emergent contact illustration

Unified Continuum Fluid-Structure Interaction - fixed-mesh variant, implicit/emergent contact illustration

Section: Possible collaboration

General planning/proposals

With the Adaptive Euler/FEniCS Open Source technology we reliably predict your aerodynamic design based on first principles. You can trust the results, and use them for decisions, optimization, redesign, etc.

General FEniCS framework for reliably and automatically predicting/simulating any mathematical model: fluid mechanics, solid mechanics, electromagnetics, chemistry, multi-physics, etc.

Easy and straightforward to yourself modify, inspect, extend. For example, you can very easily modify the Adaptive Euler FEniCS formulation into a standard WMLES formulation with explicity friction and turbulence modeling and also run that.

Good validation at the highest level and at the same time 300x-1000x faster and cheaper than the best CFD in the world: RANS and WMLES in NASA/AIAA High Lift Prediction Workshop, "zero" computational cost.

Plug-in component in your CAE/aero workflow, can reuse CAD, mesh generation, visualization.

We can provide reliable first-principles aero-data for any aircraft, e.g. certification of full aircraft, drones, new aircraft concepts, etc.

"Transient adjoint" indicates where design should be modified for maximum gain.

Contact: Johan Jansson jjan@kth.se
http://digitalmath.tech
http://icarusmath.com

Section: Solving the reproducibility crisis

Problem: Publications are not reproducible

KI President Ottersen describes the problem concisely;

We are in the midst of what some have called a research reproducibility crisis. While scientific discovery and complexity are developing at an unprecedented speed, less than 50% of scientific research studies can be reliably replicated. Left unchecked, this troubling fact may threaten our ability to generate sound, evidence-based knowledge that meets society’s needs. It is time to look beyond the traditional measures of quality and re-examine the very concept of quality itself.

NASA Transform to Open Science (TOPS):
https://science.nasa.gov/open-science/transform-to-open-science
"Lowering barriers to entry for historically excluded communities"
"Increasing opportunities for collaboration while promoting scientific innovation, transparency, and reproducibility.

Illustration: In school one may not only give the answer to a problem - "show your work!".

In research it is often not possible to see or reproduce how the answer was derived or constructed. Why is this so?

Report from European Commission

"Reproducibility of scientific results in the EU", Directorate-General for Research and Innovation (European Commission), 2020

Excerpts from the EU report:

Second, there is a perceived deliberateness, or at least carelessness, in scientific production due to competitive pressures. A growing proportion of scientists are perceived as – willingly or unwittingly – bending some of the basic premises of the scientific method to produce ‘fast science’ or even ‘make believe science’ – facts and theories that are declared true but are dubious or even false. This rests more on the structure of incentives of science-making, embedded in culture and practice, than on deliberate attempts to ‘cheat’. The need for results to be reproducible, and the tangible steps needed to make them so, may help results be trustworthy and keep scientists honest.

Possible remedies:
[...]
Sharing of data, protocols, materials, software, codes, and other tools underlying publications; Transparency of analysis and modelling;

Possible actions:
[...]
17. Fund the testing and R&I development of automatic systems of compliance for reproducibility before publication;
[...]
24. Ensure that Horizon Europe provisions encourage and support
reproducibility (see list of possible actions, above);
25. Employ and police guidelines early in the grant application phase to anchor journal practices;

etc.

Reproducibility in the digital age

Lorena Barba, a professor at George Washington University in Washington, D. C., says in Physics World:

What we are calling for is changing those norms to give importance to the full set of digital objects that are part of a scientific study and acknowledging that the scientific paper is insufficient today in its methods section to include all of the information needed for another researcher to confirm the results or build from those results.

The technology exists to achieve this, there have been technical solutions since the 80s and 90s.

In the US there are now guidelines for requiring the publication of the "digital objects" (Open Source), in the US National Academies of Sciences, Engineering and Medicine. Professor Barba has been a leader in these developments.

Zenodo (https://en.wikipedia.org/wiki/Zenodo) has become a standard resource in science for publishing “data sets”. For each submission, a persistent digital object identifier (DOI) is minted, which makes the stored items easily citeable. Zenodo is based on the Open Source project Invenio.

KTH Library is active in developing an Invenio/Zenodo-framework for supporting reproducibility.

Reproducibility in scientific modeling

With Invenio/Zenodo, DOIs can be acquired for both the source code and generated data for a scientific model, allowing this material to be easily cited. The material may then be shared while avoiding questions about ownership of the intellectual property.

However, just publishing a “data set” or even an archive of the source code, does not guarantee or make scientific results reproducible. It may still take an enormous effort to actually re-run the computations (e.g. lacking familiarity with required software, access to computing resources, etc.), and you do not know before you invest that effort how reproducible the results are (e.g. limited or missing methodology sections).

Reproducibility requires transparency. A lack of transparency in experiments creates a barrier to inclusivity and accessibility in science.

Solution

We present the Digital Math framework as the foundation for modern science based on constructive digital mathematical computation.

Ubiquitous High Performance Computing: "Copy a lab"

• "One click" - Jupyter - Google Colab - MyBinder
• Virtual Machines - Universal computing environment - HPC with 100s-1000s cores.

Easily accessible - “copy our lab at zero cost - rerun experiment in seconds 1-click in web browser”
Advantage of digital and simulation over experiments

Run and modify the simulations yourself i

Run and modify the simulations yourself in your web browser!

Solving the reproducibility crisis with Digital Math - "The Modern Scientific Paper". More detailed presentation and results:

http://digitalmath.tech/hiliftpw4-aiaa

Cylinder Re=Infinite starting from u=0

Resolution of D'Alembert's paradox: with unsteady Euler potential solution first establishes, but is unstable and develops into streamwise vortex solution, with non-zero drag close to experiment (see slides before)

Cylinder Re sweep from Re=4e3 to Re=Infinite (e.g. 1e7+)

Cylinder Re sweep from Re=4e3 to Re=Infinite (e.g. 1e7+)

Ubiquitous High Performance Computing (UHPC)

• "One click" - Jupyter - Google Colab - MyBinder
• Virtual Machines - Universal computing environment - HPC with 10s-1000s cores.
• Breakthrough: Most expensive computation (HiLift) now possible in Jupyter/Google Colab with 20 cores and 4-24 hours 100-1000 core hours.

Section: DigiMat solving the Math/STEM education crisis

DigiMat

• New revolutionary way to learn math + coding.
• For all levels.
• Creative and high impact activities developed by leading scientists.

http://digimat.tech    Johan Jansson jjan@kth.se

DigiMat Pro

Our automated framework with high-level math notation now de-facto world standard, and is now available in a web-based environment (see above). Predict, visualize, inspect, modify the math source code interactively at the highest echelon in the world, e.g. electric aircraft in the Vinnova ELISE project above.

Learn Digital Math from scratch in our DigiMat program.

Euler overview paper

Adaptive Euler as a solution to NASA Vision 2030

1. Emphasis on physics-based, predictive modeling:
Predictive - first-principles, parameter-free, adjoint-based adaptivity

2. Management of errors and uncertainties resulting from all possible sources:
Same as 1, additionally automatically generates low-level source code from math notation

3. A much higher degree of automation in all steps of the analysis process:
Same as 1 and 2

4. Ability to effectively utilize massively parallel, heterogeneous, and fault-tolerant HPC architectures:
Extremely cheap and fast performance (less than 200 core hours),

5. Flexibility to tackle capability- and capacity-computing tasks in both industrial and research environments
Same as 4

6. Seamless integration with multidisciplinary analyses that will be the norm in 2030
Digital Math/FEniCS general framework for PDE (FSI etc.)

Discussion

• Proposed Adaptive Euler as solution to the NASA Vision 2030 challenges.
• Predictive incompressible unsteady Euler - first principles - no modeling parameters.
• Extremely fast and cheap: < 100 core hours - "zero" computational cost
• Coarse mesh from ANSA/Helden: 100k vertices giving good validation for full aircraft.
• Vision: Design and certification of aircraft and engineering systems should be done by simulation (e.g. Digital Math Euler Real Flight Simulator) within 5 years.
• Free slip BC: models the very small skin friction beyond drag crisis at Re ~500000
• Unified Continuum (UC) methodology for general Fluid-Structure Interaction (FSI), validation results for biomechanics applications.
• Prototype development of Adaptive Euler for aeroelasticity in collaboration with Saab, initial aerospace results of plunge and pitch, buffeting (HLPW5), etc.

Conclusion

• We can with first principles predictive Adaptive Euler predict the forces for the sweep of aoa=7 through aoa=21.5, and moments, within 5% of experiment (10% for moments and at stall angle) under adjoint-based adaptive error control.

Perspectives

• The Euler approach represents a paradigm shift in fluid mechanics, giving a first-principles approach, and resolving the challenges described in NASA Vision 2030
• The Euler approach matches the experiments to expected accuracy, and gives comparable validation results to other WMLES results, but 1000x faster and cheaper, with adaptive error control, and with no manual/explicit parameters to tune.

Contact: Johan Jansson jjan@kth.se
http://digitalmath.tech http://icarusmath.com

You're welcome to get involved!
Try yourself, modify, extend!
http://digitalmath.tech/aero-breakthrough

Commercial cooperation:
http://icarusmath.com

Any questions, ideas, comments:
jjan@kth.se

References - IVA highlight of DigiMat

https://www.linkedin.com/feed/update/urn:li:activity:6925366593916936192/

References - Swedish Engineers highlight of DigiMat

https://twitter.com/UlrikaLindstr/status/1517133800999858176

Adjoint velocity $\hat{\phi}$ and Residual $R(\hat{U})$ (left column)
Coarse starting mesh and Refined mesh 5 adapt. it. (right column)

Adaptive error control for fixed aoa=7

Both CD and CL within 5% of exp, CM within 10%, mesh-independent

Cylinder Re sweep from Re=4e3 to Re=Infinite (e.g. 1e7+)

Formula 1 - Pilot project with leading team
(joint work with Torbjörn Larsson former Ferrari/BMW Head of CFD)

CD and CL within 4%

DrivAer standard automotive benchmark with transient adjoint

Real Unified Continuum modeling

The methodology is a Direct FEM simulation of the first principle equations, here in multi-phase incompressible form, where we include constitutive laws for a Newtonian fluid and Neo-Hookean solid.

These first principle equations are discretized by the Direct FEM approach, meaning Galerkin-Least-Squares (GLS) stabilization with shock-capturing.

The Galerkin part of the method is formulated as below in FEniCS notation:

F_G = z*inner(u, grad(rho))*nu*dx
F_G += z*(inner(rho*grad(u)*u + grad(p),v) - theta*inner(sigma, grad(v)) + \
    nnu*inner(grad(u),grad(v)) - rho*dot(f,v))*dx
F_G += z*(inner(dot(u, grad(sigma)) + \
    theta*(2*rho*mumu*epsilon(u) + grad(u)*sigma + sigma*grad(u).T), y))*dx

Building aerodynamics

Master thesis by Linde van Beers supervised by Johan Jansson.

Multiphase - marine - flooding

Formula 1 - Perrinn benchmark
(joint work with Torbjörn Larsson former Ferrari/Red Bull Head of CFD)

CD and CL within 4%

IEA-OES benchmark project on wave energy

Adaptive error control for fixed aoa=21.5 (fine surface mesh)

CD, CL and CM within 10% of exp, mesh-independent

Snapshot of adjoint solution (green) for aoa=21.5

Showing sensitivity in nacelle and wing-root region

Snapshot of adjoint solution (green) for aoa=21.5

Showing sensitivity in nacelle and wing-root region

Cylinder Re sweep from Re=4e3 to Re=Infinite (e.g. 1e7+)

Adaptive Euler Unified Compressible Mach=0.2

Adaptive Euler Unified Compressible Mach=0.7

Adaptive Euler Unified Compressible Mach=2.0

Adaptive Euler Unified Compressible

Glider Optimal Sustainable Mobility

Project Glider develops a world-unique and efficient mobility solution based on gliding for the transport of people and goods. With gliding, neither energy storage (petrol, battery, etc.) nor engine is required on the craft, which brings enormous gains in weight, cost, complexity and durability. Gliding has been used militarily (largely during WWII) and today is mostly used for recreation. We see that gliding has great potential for large-scale sustainable movement of goods and people, as a sustainable mobility system for society.

Aviation today accounts for 2% of global carbon dioxide emissions, and the share is expected to increase to 15-27% by 2050. We are already a leader in electric flight research through our role in the ELISE project. Gliders mean even greater opportunities for sustainable mobility in that the problem of energy storage on the craft is eliminated.

Glider Optimal Sustainable Mobility

The technical idea is that the gliders are launched by e.g. an electric car or truck, or by an electric induction-based “launcher” similar to the established railgun technology used e.g. to launch aircraft from carriers. The glider aircraft can then glide 100km-200km, and can then be relaunched, or be provided with energy by induction at “energy stations”, eliminating the need for landing and relaunch.

A design variant can be that the glider aircraft have solar panels and a simple electric propulsion. With the efficient aerodynamics provided by our Adaptive Euler simulation-based design, and potentially by leveraging Ground Effect - giving appx. 2x higher efficiency, it appears possible to achieve “infinite range” with a simple solar-based solution.

FEniCS component structure

Note that Adaptive Euler depends on DOLFIN, FFC, PETSc (linear algebra), etc. large and global Open Source communities similar to Linux

We have good contact with PETSc (linear algebra) development team (Matt Knepley), and with e.g. recent large community around NURBS/spline FEM (David Kamensky).

Preliminary Adaptive Euler Compressible - qualitative validation against Adaptive Euler Incompressible HLPW5 aoa=19.7

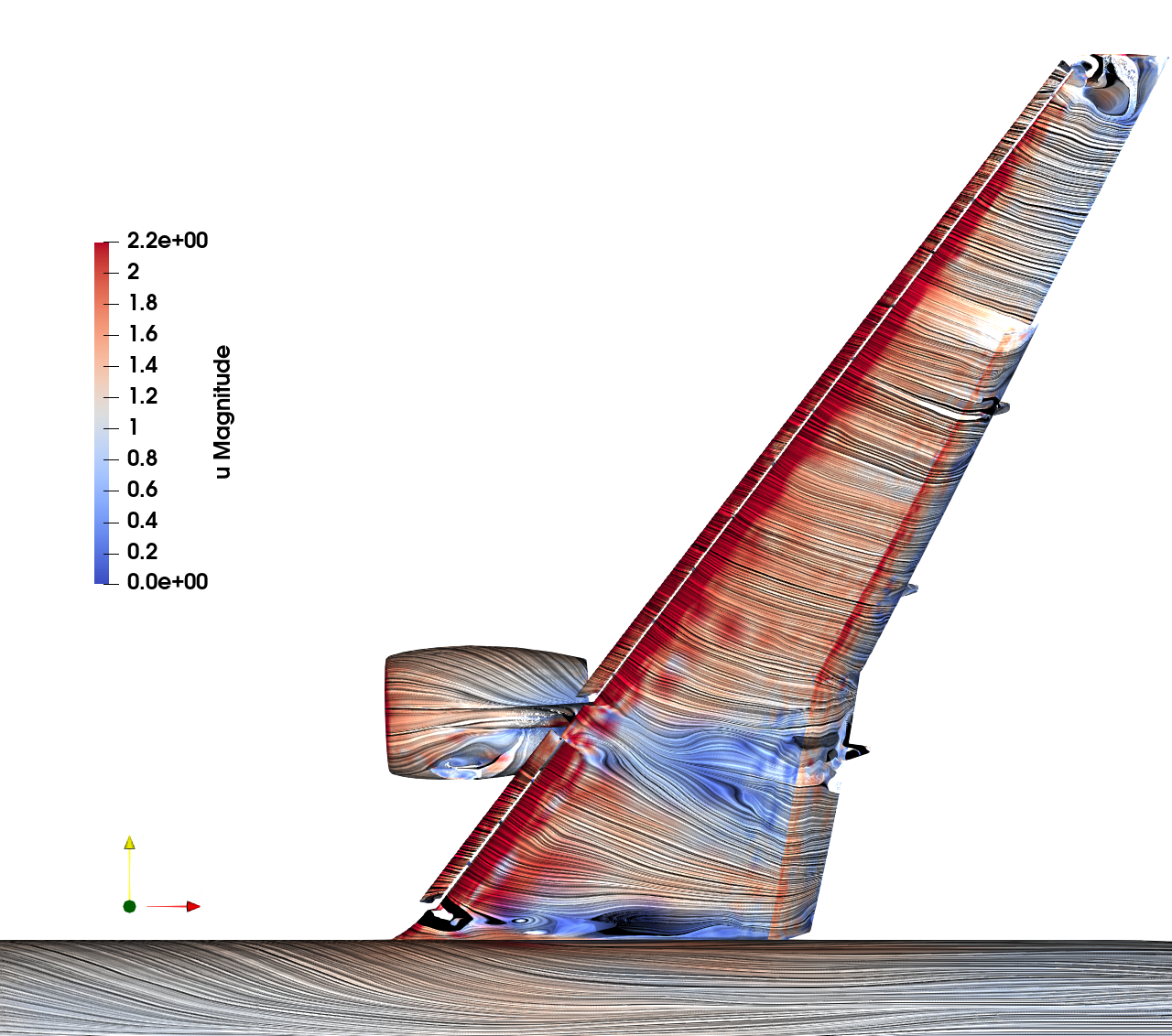
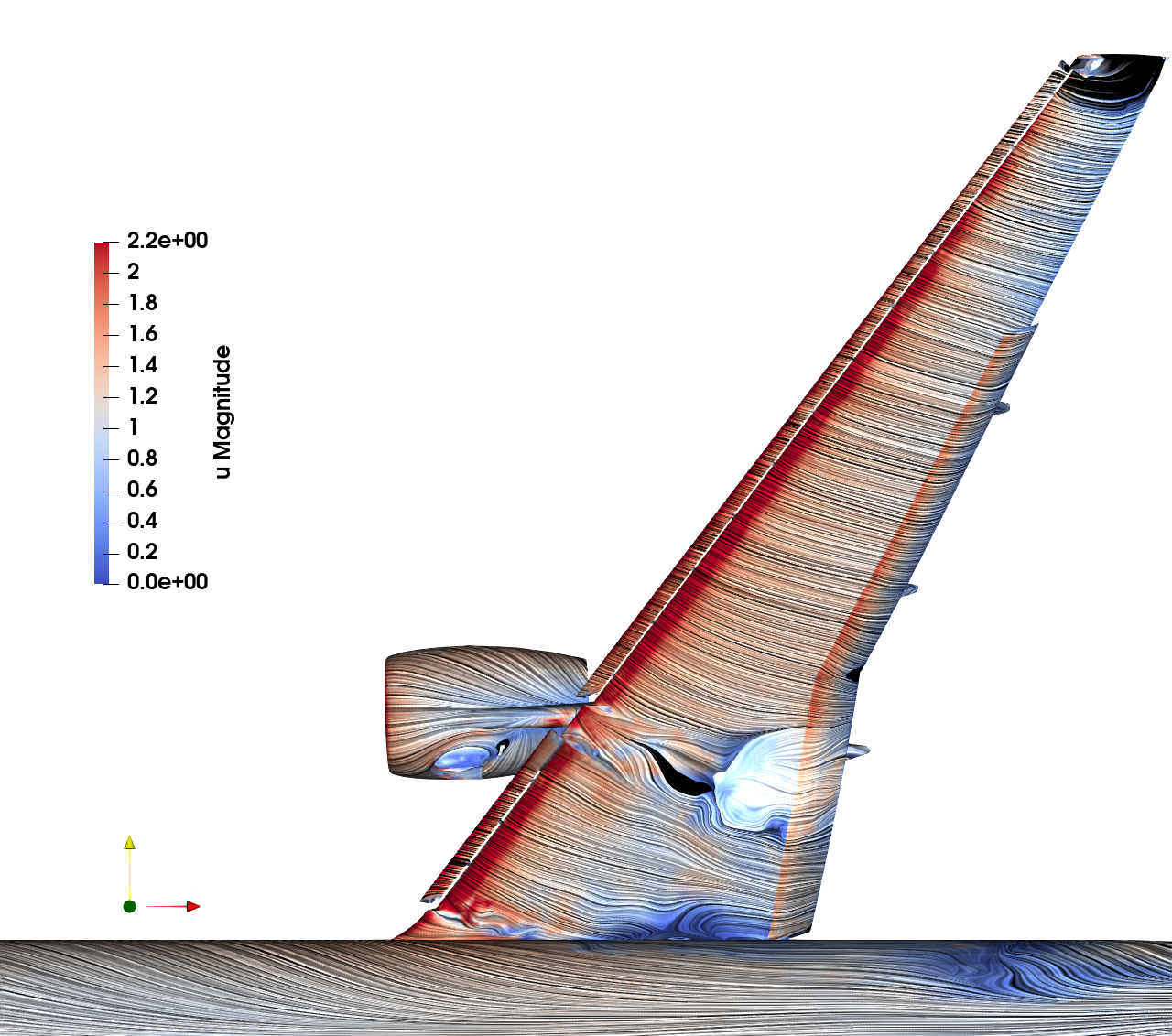
Movie of velocity and motion Adaptive Euler PAPA prototype

Forces Adaptive Euler PAPA prototype 2023-12-08_01

Computational efficiency: 20 minutes on 80 core computer (less than 1h on typical workstation)

Adaptive error control Euler PAPA prototype: Adjoint velocity and adapted mesh for adaptive iter_00 to iter_02